在此感谢Carl哥的算法平台——【代码随想录 】
来自大三的我:才意识到算法的重要性 !
大一、大二时期没有对算法重视起来,导致算法基础比较差,前段时间为了蓝桥杯比赛才稍微系统的学习了一下,象征性的刷了些题,只能说现在能看出来用什么,但不熟练,不会拓宽思维!
现在重新跟着Carl哥学一下,为了备战实习和秋招,每天分出3-4小时学习算法!
upd:小Tips:对于第一次使用或不经常使用lc的小伙伴,可能习惯了acm的方式做算法题,如果遇到报错情况不知道怎么解决,结合AI工具是个提高效率的好办法!
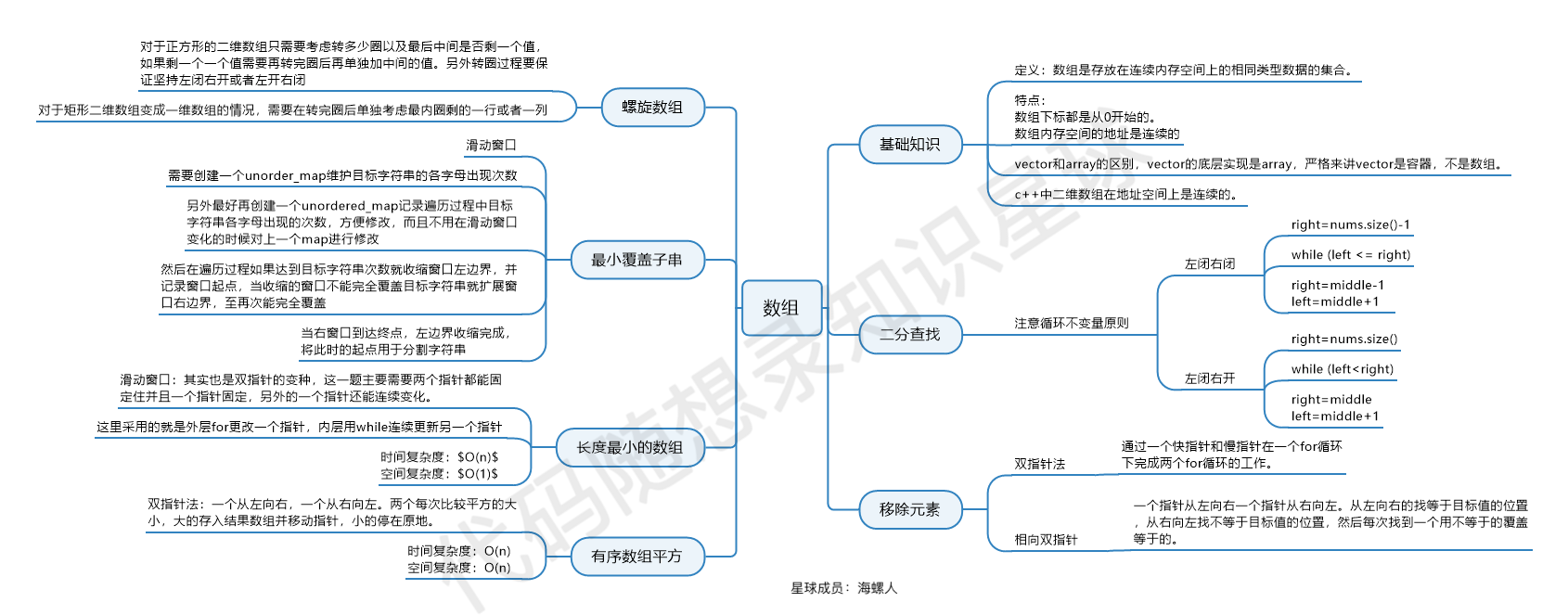
数组
二分查找
704. 二分查找 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : int search (vector<int >& nums, int target) int l = -1 ,r = nums.size (); while (l+1 <r){ int mid = (l+r)>>1 ; if (nums[mid]<target)l = mid; else if (nums[mid]>target)r = mid; else return mid; } return -1 ; } };
35. 搜索插入位置 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 class Solution {public : int searchInsert (vector<int >& nums, int target) int l = -1 ,r = nums.size (); while (l+1 <r){ int mid = (l+r)>>1 ; if (nums[mid]<target)l = mid; else r = mid; } return r; } };
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
注意如果target大于数组中所有数的情况下,r会角标越界的情况。
之前不经常用vector容器没注意到这个问题 ,lc给我报的错
1 2 Line 1034 : Char 9 : runtime error: reference binding to null pointer of type 'int' (stl_vector.h) SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior /usr/ bin/../ lib/gcc/ x86_64-linux-gnu/9/ ../../ ../../i nclude/c++/ 9 /bits/ stl_vector.h:1043 :9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution {public : int search_left (vector<int >& nums,int target) int l = -1 ,r = nums.size (); while (l+1 <r){ int mid = (l+r)>>1 ; if (nums[mid]<target)l = mid; else r = mid; } if (r<nums.size () && nums[r] == target)return r; else return -1 ; } int search_right (vector<int >& nums,int target) int l = -1 ,r = nums.size (); while (l+1 <r){ int mid = (l+r)>>1 ; if (nums[mid]<=target)l = mid; else r = mid; } if (l>=0 && nums[l] == target)return l; else return -1 ; } vector<int > searchRange (vector<int >& nums, int target) { int ans1,ans2; ans1 = search_left (nums,target); ans2 = search_right (nums,target); return {ans1,ans2}; } };
69. x 的平方根 - 力扣(LeetCode)
注意 使用该板子要特判边界
mid<=x/mid 防止溢出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : int mySqrt (int x) if (x == 0 )return 0 ; if (x == 1 )return 1 ; long l = 0 ,r = x; while (l+1 <r){ int mid = (l+r)>>1 ; if (mid<=x/mid)l = mid; else r = mid; } return l; } };
367. 有效的完全平方数 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int check (int num) if (num == 0 )return 0 ; if (num == 1 )return 1 ; int l = 0 ,r = num; while (l+1 <r){ int mid = (l+r)>>1 ; if (mid<=num/mid)l = mid; else r = mid; } return l; } bool isPerfectSquare (int num) int ans = check (num); if (ans * ans == num)return true ; else return false ; } };
移除元素
27. 移除元素 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : int removeElement (vector<int >& nums, int val) int size = nums.size (); for (int i = 0 ; i < size; i++) { if (nums[i] == val) { for (int j = i + 1 ; j < size; j++) { nums[j - 1 ] = nums[j]; } i--; size--; } } return size; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : int removeElement (vector<int >& nums, int val) int size = nums.size (); int j = 0 ; for (int i = 0 ;i<size;i++){ if (val != nums[i]){ nums[j++] = nums[i]; } } return j; } };
26. 删除有序数组中的重复项 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : int removeDuplicates (vector<int >& nums) int len = nums.size (); if (len == 0 )return 0 ; int i = 1 ,j = 0 ; while (i<len){ if (nums[i] != nums[j]){ nums[++j] = nums[i]; } i++; } return j+1 ; } };
283. 移动零 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : void moveZeroes (vector<int >& nums) int i = 0 ,j = 0 ; int len = nums.size (); if (len == 1 )return ; while (i < len){ if (nums[i] != 0 )swap (nums[i],nums[j++]); i++; } } };
844. 比较含退格的字符串 - 力扣(LeetCode)
初步想法 快慢指针
j>0这个条件要加上,否则会越界 对于下面这个用例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : string check (string s) { int len = s.size (); int i = 0 ,j = 0 ; while (i<len){ if (s[i] != '#' )s[j++] = s[i]; else if (j>0 ) j--; i++; } return s.substr (0 ,j); } bool backspaceCompare (string s, string t) return check (s) == check (t); } };
有序数组的平方
977. 有序数组的平方 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 lass Solution { public : vector<int > sortedSquares (vector<int >& A) { for (int i = 0 ; i < A.size (); i++) { A[i] *= A[i]; } sort (A.begin (), A.end ()); return A; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : vector<int > sortedSquares (vector<int >& A) { int k = A.size () - 1 ; vector<int > result (A.size()) ; for (int i = 0 , j = A.size () - 1 ; i <= j;) { if (A[i] * A[i] < A[j] * A[j]) { result[k--] = A[j] * A[j]; j--; } else { result[k--] = A[i] * A[i]; i++; } } return result; } };
长度最小的子数组
209. 长度最小的子数组 - 力扣(LeetCode)
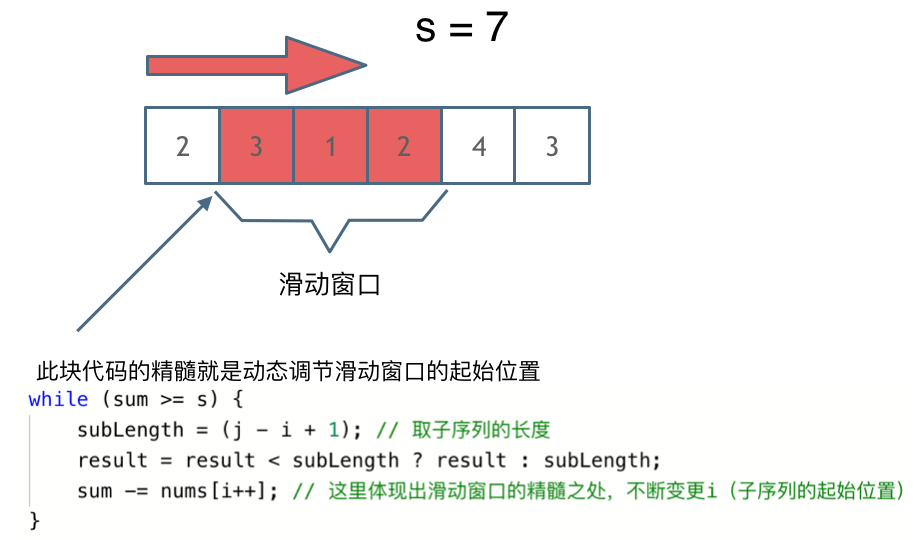
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : int minSubArrayLen (int target, vector<int >& nums) int sum = 0 ; int res = 1e5 +10 ; int i = 0 ; int max_len; int len = nums.size (); for (int j = 0 ; j<len;j++){ sum+=nums[j]; while (sum>=target){ max_len = j-i+1 ; res = min (res,max_len); sum = sum-nums[i++]; } } return res == 1e5 +10 ?0 :res; } };
904. 水果成篮 - 力扣(LeetCode)
目的是找到两个数,使得这两个数字出现的次数最多且是连续的,只需要从左到右遍历左边,将其加入哈希表中,如果此时哈希表的数字种类超过2,依次删除哈希表里面的数字种类,如果种类为零 则擦除该数,依次遍历即可最后返回最大长度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : int totalFruit (vector<int >& fruits) int i = 0 ,j = 0 ; int len = fruits.size (); int ans = -1 ; map<int ,int >mp; for (i = 0 ;i < len;i++){ mp[fruits[i]]++; while (mp.size ()>2 ){ auto it = mp.find (fruits[j]); it->second--; if (it->second == 0 ) mp.erase (it); j++; } ans = max (ans,i-j+1 ); } return ans; } };
76. 最小覆盖子串 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution {public : vector<vector<int >> generateMatrix (int n) { vector<vector<int >> matrix (n, vector <int >(n, 0 )); int num = 1 ; int top = 0 , bottom = n - 1 , left = 0 , right = n - 1 ; while (num <= n * n) { for (int col = left; col <= right; col++) { matrix[top][col] = num++; } top++; for (int row = top; row <= bottom; row++) { matrix[row][right] = num++; } right--; for (int col = right; col >= left; col--) { matrix[bottom][col] = num++; } bottom--; for (int row = bottom; row >= top; row--) { matrix[row][left] = num++; } left++; } return matrix; } };
54. 螺旋矩阵 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution {public : vector<int > spiralOrder (vector<vector<int >>& matrix) { vector<int >arr; if (matrix.empty ())return arr; int top = 0 ; int bottom = matrix.size ()-1 ; int left = 0 ; int right = matrix[0 ].size ()-1 ; while (1 ){ for (int j = left;j <= right;j++)arr.push_back (matrix[top][j]); if (++top>bottom)break ; for (int i = top;i <= bottom;i++)arr.push_back (matrix[i][right]); if (--right<left)break ; for (int j = right;j>=left;j--)arr.push_back (matrix[bottom][j]); if (--bottom<top)break ; for (int i = bottom;i>=top;i--)arr.push_back (matrix[i][left]); if (++left>right)break ; } return arr; } };
LCR 146. 螺旋遍历二维数组 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution {public : vector<int > spiralArray (vector<vector<int >>& array) { vector<int >arr; if (array.empty ())return arr; int top = 0 ; int bottom = array.size ()-1 ; int left = 0 ; int right = array[0 ].size ()-1 ; while (1 ){ for (int j = left;j<=right;j++)arr.push_back (array[top][j]); if (++top>bottom)break ; for (int i = top;i<=bottom;i++)arr.push_back (array[i][right]); if (--right<left)break ; for (int j = right;j>=left;j--)arr.push_back (array[bottom][j]); if (--bottom<top)break ; for (int i = bottom;i>=top;i--)arr.push_back (array[i][left]); if (++left>right)break ; } return arr; } };
总结
链表
链表理论基础
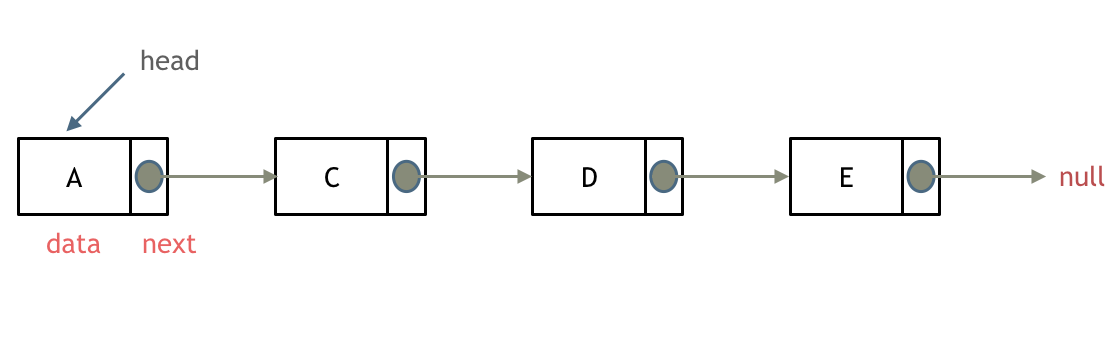
链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。
链表的类型
链表存储方式
链表的定义
1 2 3 4 5 6 struct ListNode { int val; ListNode *next; ListNode (int x) : val (x), next (NULL ) {} };
移除链表元素
203. 移除链表元素 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : ListNode* removeElements (ListNode* head, int val) { ListNode *dummyHead = new ListNode (0 ); dummyHead->next = head; ListNode *cur = dummyHead; while (cur->next != nullptr ){ if (cur->next->val == val){ ListNode *tmp = cur->next; cur->next = cur->next->next; delete tmp; }else { cur =cur->next; } } head = dummyHead->next; delete dummyHead; return head; } };
设计链表
707. 设计链表 - 力扣(LeetCode)
这道题目设计链表的五个接口:
获取链表第index个节点的数值
在链表的最前面插入一个节点
在链表的最后面插入一个节点
在链表第index个节点前面插入一个节点
删除链表的第index个节点
AC代码(LinkedNode硬是写成ListNode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 class MyLinkedList {public : struct ListNode { int val; ListNode *next; ListNode (int x):val (x),next (nullptr ){}; }; MyLinkedList () { dummyHead = new ListNode (0 ); List_Size = 0 ; } int get (int index) if (index > List_Size-1 || List_Size < 0 ) return -1 ; ListNode *cur = dummyHead->next; while (index --){ cur = cur->next; } return cur->val; } void addAtHead (int val) ListNode *newNode = new ListNode (val); newNode->next = dummyHead->next; dummyHead->next = newNode; List_Size++; } void addAtTail (int val) ListNode *newNode = new ListNode (val); ListNode *cur = dummyHead; while (cur->next != NULL ){ cur = cur->next; } cur->next = newNode; List_Size++; } void addAtIndex (int index, int val) if (index > List_Size) return ; if (index < 0 ) index = 0 ; ListNode *newNode = new ListNode (val); ListNode *cur = dummyHead; while (index --){ cur = cur->next; } newNode->next = cur->next; cur->next = newNode; List_Size++; } void deleteAtIndex (int index) if (index > List_Size-1 || List_Size<0 ) return ; ListNode *cur = dummyHead; while (index --){ cur = cur->next; } ListNode *tmp = cur->next; cur->next = cur->next->next; delete tmp; tmp = NULL ; List_Size--; } private : int List_Size; ListNode* dummyHead; };
1 2 3 4 Line 26: Char 36: runtime error: member access within misaligned address 0xbebebebebebebebe for type 'ListNode' , which requires 8 byte alignment (solution.cpp) 0xbebebebebebebebe: note: pointer points here <memory cannot be printed> SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior prog_joined.cpp:31:36
错误原因:存在未定义行为,具体是成员访问在未对齐的地址上
排查:
MyLinkedList() {
ListNode *dummyHead = new ListNode(0); // 不应该加ListNode
List_Size = 0;
}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 class MyLinkedList {public : struct LinkedNode { int val; LinkedNode* next; LinkedNode (int val):val (val), next (nullptr ){} }; MyLinkedList () { _dummyHead = new LinkedNode (0 ); _size = 0 ; } int get (int index) if (index > (_size - 1 ) || index < 0 ) { return -1 ; } LinkedNode* cur = _dummyHead->next; while (index--){ cur = cur->next; } return cur->val; } void addAtHead (int val) LinkedNode* newNode = new LinkedNode (val); newNode->next = _dummyHead->next; _dummyHead->next = newNode; _size++; } void addAtTail (int val) LinkedNode* newNode = new LinkedNode (val); LinkedNode* cur = _dummyHead; while (cur->next != nullptr ){ cur = cur->next; } cur->next = newNode; _size++; } void addAtIndex (int index, int val) if (index > _size) return ; if (index < 0 ) index = 0 ; LinkedNode* newNode = new LinkedNode (val); LinkedNode* cur = _dummyHead; while (index--) { cur = cur->next; } newNode->next = cur->next; cur->next = newNode; _size++; } void deleteAtIndex (int index) if (index >= _size || index < 0 ) { return ; } LinkedNode* cur = _dummyHead; while (index--) { cur = cur ->next; } LinkedNode* tmp = cur->next; cur->next = cur->next->next; delete tmp; tmp=nullptr ; _size--; } void printLinkedList () LinkedNode* cur = _dummyHead; while (cur->next != nullptr ) { cout << cur->next->val << " " ; cur = cur->next; } cout << endl; } private : int _size; LinkedNode* _dummyHead; };
反转链表
206.反转链表 - 力扣(LeetCode)
思路:改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : ListNode* reverseList (ListNode* head) { ListNode* tmp ; ListNode* cur = head; ListNode* pre = nullptr ; while (cur){ tmp = cur->next; cur->next = pre; pre = cur; cur = tmp; } return pre; } };
两两交换链表中的节点
24. 两两交换链表中的节点 - 力扣(LeetCode)
思路:画图模拟 用两个tmp记录临时节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : ListNode* swapPairs (ListNode* head) { ListNode* dummyHead = new ListNode (0 ); dummyHead->next=head; ListNode* cur = dummyHead; while (cur->next != nullptr && cur->next->next != nullptr ){ ListNode* tmp1 = cur->next; ListNode* tmp2 = cur->next->next->next; cur->next = cur->next->next; cur->next->next = tmp1; cur->next->next->next = tmp2; cur = cur->next->next; } ListNode* res = dummyHead->next; delete dummyHead; return res; } };
删除链表的倒数第 N 个结点
19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)
思路: 双指针 画图模拟
定义fast指针和slow指针,初始值为虚拟头结点,如图:
fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
fast和slow同时移动,直到fast指向末尾,如题:
删除slow指向的下一个节点,如图:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : ListNode* removeNthFromEnd (ListNode* head, int n) { ListNode* dummyHead = new ListNode (0 ); dummyHead->next = head; ListNode* i = dummyHead; ListNode* j = dummyHead; while (n-- && i->next != nullptr ){ i = i->next; } i = i->next; while (i != nullptr ){ i = i->next; j = j->next; } j -> next = j->next->next; return dummyHead->next; } };
tip: return dummyHead->next 而不能直接return head
直接return head 当链表为空时会报错!
链表相交
面试题 02.07. 链表相交 - 力扣(LeetCode)
思路:
考虑到重复的链表节点一定一样长,所以只需要从后往前保留一样长度即可
curA指向链表A的头结点,curB指向链表B的头结点
求出链表长度,计算差值,然后让curA移动到,和curB 末尾对齐的位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : ListNode *getIntersectionNode (ListNode *headA, ListNode *headB) { ListNode* cur1 = headA; ListNode* cur2 = headB; int len1 = 0 ,len2 = 0 ; while (cur1 != NULL ){ len1++; cur1 = cur1->next; } while (cur2 != NULL ){ len2++; cur2 = cur2->next; } cur1 = headA; cur2 = headB; if (len2>len1){ swap (cur1,cur2); } int len = abs (len1-len2); while (len--){ cur1 = cur1->next; } while (cur1 != NULL ){ if (cur1 == cur2) return cur1; cur1 = cur1->next; cur2 = cur2->next; } return NULL ; } };
环形链表II
142. 环形链表 II - 力扣(LeetCode)
思路 代码随想录
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : ListNode *detectCycle (ListNode *head) { ListNode* fast = head; ListNode* slow = head; while (fast != NULL && fast->next != NULL ) { slow = slow->next; fast = fast->next->next; if (slow == fast) { ListNode* index1 = fast; ListNode* index2 = head; while (index1 != index2) { index1 = index1->next; index2 = index2->next; } return index2; } } return NULL ; } };
遍历链表,第一次遇到就把结点放进集合(注意放的是地址不是值),后面如果再次遍历到说明有环,返回遍历到的第一个重复结点的位置就可以了,如果循环能够结束说明有空指针域(即一定无环),因此最后返回NULL就可以了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : ListNode *detectCycle (ListNode *head) { ListNode* cur = head; set<ListNode*> s; while (cur){ if (s.find (cur) != s.end ()) return cur; s.insert (cur); cur = cur->next; } return NULL ; } };
哈希表
哈希表理论基础
代码随想录-哈希表理论基础
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法 。
有效的字母异位词
242. 有效的字母异位词 - 力扣(LeetCode)
思路:数组存储每个字母出现的次数,最后扣减
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : bool isAnagram (string s, string t) int flag[30 ] = {0 }; for (int i = 0 ; i<s.size ();i++){ flag[s[i]-'a' ]++; } for (int i = 0 ; i<t.size ();i++){ flag[t[i]-'a' ]--; } for (int i = 0 ; i<26 ;i++){ if (flag[i] != 0 ) return false ; } return true ; } };
字母异位词分组
49. 字母异位词分组 - 力扣(LeetCode)
思路:
特征分类->哈希表
特征分类:aab,aba,baa从小到大排序可以得到同一个字符串aab;而对于abb,bab来说排序后为abb,不等于aab;所以当且仅当两个字符串排序后一样,这样两个字符串才能分到同一组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : vector<vector<string>> groupAnagrams (vector<string>& strs) { unordered_map<string,vector<string>> mp; for (auto s:strs){ string sort_s = s; sort (sort_s.begin (),sort_s.end ()); mp[sort_s].push_back (s); } vector<vector<string>> ans; for (auto t : mp){ ans.push_back (t.second); } return ans; } };
找到字符串中所有字母异位词
438. 找到字符串中所有字母异位词 - 力扣(LeetCode)
思路:438. 找到字符串中所有字母异位词 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public : vector<int > findAnagrams (string s, string p) { unordered_map<char ,int >need ,widow; for (char c:p)need[c]++; int l,r = 0 ; int valid = 0 ; vector<int > ans; while (r<s.size ()){ char c = s[r]; r++; if (need.count (c)){ widow[c]++; if (widow[c] == need[c]) valid++; } while (r - l >= p.size ()){ if (valid == need.size ()) ans.push_back (l); char d = s[l]; l++; if (need.count (d)){ if (widow[d] == need[d]) valid--; widow[d]--; } } } return ans; } };
两个数组的交集
349. 两个数组的交集 - 力扣(LeetCode)
思路:
输出去重 SET
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : vector<int > intersection (vector<int >& nums1, vector<int >& nums2) { unordered_set<int > ans; unordered_set<int > flag (nums1. begin(),nums1. end()) ; for (auto num:nums2){ if (flag.find (num) != flag.end ()) ans.insert (num); } return vector <int >(ans.begin (),ans.end ()); } };
快乐数
202. 快乐数 - 力扣(LeetCode)
首先要计算出sum,用set记录sum,对于重复出现的sum 为进入无限循环返回false
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public : int getsum (int n) int sum = 0 ; while (n){ sum+=(n%10 )*(n%10 ); n/=10 ; } return sum; } bool isHappy (int n) unordered_set<int > st; while (true ){ int sum = getsum (n); if (sum == 1 ){ return true ; } if (st.find (sum)!= st.end ()){ return false ; }else { st.insert (sum); n = sum; } } } };
两数之和
1. 两数之和 - 力扣(LeetCode)
题干说:请你在该数组中找出 和为目标值 target两个 整数,并返回下标
也就是说只会有一组答案出现,想到用hash
因为既要返回值,又要返回值的下标,所以采用map
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : vector<int > twoSum (vector<int >& nums, int target) { unordered_map<int ,int > mp; for (int i = 0 ; i<nums.size ();i++){ auto it = mp.find (target - nums[i]); if (it!= mp.end ()) return {it->second,i}; mp.insert (pair <int , int >(nums[i], i)); } return {}; } };
四数相加II
454. 四数相加 II - 力扣(LeetCode)
题目是四个独立的数组,只要找到A[i] + B[j] + C[k] + D[l] = 0就可以,不用考虑有重复的四个元素相加等于0的情况
首先定义 一个unordered_map,key放a和b两数之和,value 放a和b两数之和出现的次数。
遍历大A和大B数组,统计两个数组元素之和,和出现的次数,放到map中。
定义int变量count,用来统计 a+b+c+d = 0 出现的次数。
在遍历大C和大D数组,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。
最后返回统计值 count 就可以了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int fourSumCount (vector<int >& nums1, vector<int >& nums2, vector<int >& nums3, vector<int >& nums4) map<int ,int > mp; int ans = 0 ; for (auto a:nums1){ for (auto b:nums2){ mp[a+b]++; } } for (auto c: nums3){ for (auto d:nums4){ if (mp.find (0 -(c+d)) != mp.end ()) ans += mp[0 -(c+d)]; } } return ans; } };
赎金信
383. 赎金信 - 力扣(LeetCode)
从 str2 找 str1 所以要先记录str2
特判 str1>str2 返回false
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : bool canConstruct (string ransomNote, string magazine) int flag[26 ] = {0 }; if (ransomNote.size ()>magazine.size ())return false ; for (int i =0 ; i<magazine.size ();i++){ flag[magazine[i]-'a' ]++; } for (int i = 0 ;i<ransomNote.size ();i++){ flag[ransomNote[i]-'a' ]--; if (flag[ransomNote[i]-'a' ] < 0 )return false ; } return true ; } };
总结
一般来说哈希表都是用来快速判断一个元素是否出现集合里 。
三种哈希结构:
考虑好什么情况下用数组 ,什么情况下用set/map,选择合适的!
字符串
反转字符串
344. 反转字符串 - 力扣(LeetCode)
双指针
1 2 3 4 5 6 7 8 9 class Solution {public : void reverseString (vector<char >& s) int i = 0 ,j = s.size ()-1 ; while (i<j){ swap (s[i++],s[j--]); } } };
反转字符串II
541. 反转字符串 II - 力扣(LeetCode)
当需要固定规律一段一段去处理字符串的时候,要想想在在for循环的表达式上做做文章 对于这道题而言,将 i 的位置每次移动 2k 即可
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : string reverseStr (string s, int k) { for (int i = 0 ; i< s.size ();i+=2 *k){ if (i+k <= s.size ()){ reverse (s.begin ()+i,s.begin ()+i+k); }else { reverse (s.begin ()+i,s.end ()); } } return s; } };
替换数字
54. 替换数字 (kamacoder.com)
最开始的思路:就是从前往后遍历,遇到数字就替换,但在一想,后面的所有数字都要重新安排 ,时间复杂度为O(n^2) 会TLE
卡哥给了我新思路(先扩充字符串大小,利用双指针从后往前替换),真的巧妙这方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> #define int long long #define endl '\n' using namespace std;signed main () string s; cin>>s; int index = s.size ()-1 ; int cnt = 0 ; for (int i = 0 ; i < s.size (); i++) { if (s[i]>='0' && s[i]<='9' )cnt++; } s.resize (s.size ()+ cnt*5 ); int NewIndex = s.size ()-1 ; for (int i = index; i >=0 ;i-- ){ if (s[i]>='0' && s[i] <= '9' ){ s[NewIndex--] = 'r' ; s[NewIndex--] = 'e' ; s[NewIndex--] = 'b' ; s[NewIndex--] = 'm' ; s[NewIndex--] = 'u' ; s[NewIndex--] = 'n' ; }else { s[NewIndex--] = s[i]; } } cout<<s<<endl; return 0 ; }
翻转字符串里的单词
151. 反转字符串中的单词 - 力扣(LeetCode)
移除多余空格 (双指针 快慢指针)
将整个字符串反转
将每个单词反转
这道题要多练习下
出错点: removespace(string s) 传的是地址而不是值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution {public : void removespace (string& s) int slow = 0 ; for (int i = 0 ; i < s.size (); ++i){ if (s[i] != ' ' ){ if (slow != 0 ) s[slow++] = ' ' ; while (i<s.size () && s[i] != ' ' ) s[slow++] = s[i++]; } } s.resize (slow); } void reverse (string& s, int start, int end) for (int i = start, j = end; i < j; i++, j--) { swap (s[i], s[j]); } } string reverseWords (string s) { removespace (s); reverse (s,0 ,s.size ()-1 ); int index = 0 ; for (int i =0 ; i <=s.size ();++i){ if (i == s.size () || s[i] == ' ' ){ reverse (s,index,i-1 ); index = i+1 ; } } return s; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 void removeExtraSpaces (string& s) int slow = 0 ; for (int i = 0 ; i < s.size (); ++i) { if (s[i] != ' ' ) { if (slow != 0 ) s[slow++] = ' ' ; while (i < s.size () && s[i] != ' ' ) { s[slow++] = s[i++]; } } } s.resize (slow); }
1 2 3 4 5 6 void reverse (string& s, int start, int end) for (int i = start, j = end; i < j; i++, j--) { swap (s[i], s[j]); } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution {public : void reverse (string& s, int start, int end) for (int i = start, j = end; i < j; i++, j--) { swap (s[i], s[j]); } } void removeExtraSpaces (string& s) int slow = 0 ; for (int i = 0 ; i < s.size (); ++i) { if (s[i] != ' ' ) { if (slow != 0 ) s[slow++] = ' ' ; while (i < s.size () && s[i] != ' ' ) { s[slow++] = s[i++]; } } } s.resize (slow); } string reverseWords (string s) { removeExtraSpaces (s); reverse (s, 0 , s.size () - 1 ); int start = 0 ; for (int i = 0 ; i <= s.size (); ++i) { if (i == s.size () || s[i] == ' ' ) { reverse (s, start, i - 1 ); start = i + 1 ; } } return s; } };
右旋字符串
55. 右旋字符串 (kamacoder.com)
翻转再翻转,划分好区间
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #include <bits/stdc++.h> #define int long long #define endl '\n' using namespace std;signed main () int n; string s; cin>>n>>s; reverse (s.begin (),s.end ()); reverse (s.begin (),s.begin ()+n); reverse (s.begin ()+n,s.end ()); cout<<s<<endl; return 0 ; }
拓展 剑指 Offer 58 - II. 左旋转字符串
LCR 182. 动态口令 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 class Solution {public : string dynamicPassword (string password, int target) { reverse (password.begin (),password.begin ()+target); reverse (password.begin ()+target,password.end ()); reverse (password.begin (),password.end ()); return password; } };
实现 strStr()
28. 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : int strStr (string haystack, string needle) int a = haystack.size (); int b = needle.size (); for (int i = 0 ; i<=a-b;i++){ int j = i, k = 0 ; while (k<b &&haystack[j] == needle[k]){ j++; k++; } if (k == b)return i; } return -1 ; } };
代码随想录 (programmercarl.com)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : void getNext (int * next, const string& s) int j = -1 ; next[0 ] = j; for (int i = 1 ; i < s.size (); i++) { while (j >= 0 && s[i] != s[j + 1 ]) { j = next[j]; } if (s[i] == s[j + 1 ]) { j++; } next[i] = j; } } int strStr (string haystack, string needle) if (needle.size () == 0 ) { return 0 ; } vector<int > next (needle.size()) ; getNext (&next[0 ], needle); int j = -1 ; for (int i = 0 ; i < haystack.size (); i++) { while (j >= 0 && haystack[i] != needle[j + 1 ]) { j = next[j]; } if (haystack[i] == needle[j + 1 ]) { j++; } if (j == (needle.size () - 1 ) ) { return (i - needle.size () + 1 ); } } return -1 ; } };
重复的子字符串
459. 重复的子字符串 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 class Solution {public : bool repeatedSubstringPattern (string s) string t = s + s; t.erase (t.begin ()); t.erase (t.end () - 1 ); if (t.find (s) != std::string::npos) return true ; return false ; } };
双指针
卡哥双指针章节的部分题目都出现在了其他以往章节里,那些题目这里就不写了
三数之和
15. 三数之和 - 力扣(LeetCode)
大致思路:
先对数组进行排序 !!!!!循环遍历,将i -> 0,left -> i+1,right -> nums.size()-1
如何移动指针
如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动(事先排过序了),这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
重点在于 如何去重
对于nums[i]来说:
是去判断nums[i] == nums[i+1],还是判断nums[i] == nums[i-1]
nums[i] == nums[i+1],会和nums[left]产生冲突,会去掉结果集中的内容,如{-1,-1,2},所以我们选择nums[i] == nums[i-1]
那left和right指针也是相同道理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public : vector<vector<int >> threeSum (vector<int >& nums) { vector<vector<int >> res; sort (nums.begin (),nums.end ()); for (int i = 0 ; i< nums.size ();i++){ if (nums[i]>0 )return res; int left = i+1 ; int right = nums.size ()-1 ; if (i>0 && nums[i] == nums[i-1 ])continue ; while (left < right){ if (nums[i]+nums[left]+nums[right]>0 )right--; else if (nums[i]+nums[left]+nums[right]<0 )left++; else { res.push_back (vector<int >{nums[i],nums[left],nums[right]}); while (left < right && nums[right] == nums[right - 1 ]) right--; while (left < right && nums[left] == nums[left + 1 ]) left++; right--; left++; } } } return res; } };
四数之和
18. 四数之和 - 力扣(LeetCode)
思路
和三数之和一样,三层循环,固定nums[k]+nums[i],移动指针寻找符合条件的nums[left]、nums[right]
但要注意target是随机值,所以剪枝的时候要重新特判 ;
nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出,开 LONG
还有千万别忘了先排序!!!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution {public : vector<vector<int >> fourSum (vector<int >& nums, int target) { vector<vector<int >> res; sort (nums.begin (),nums.end ()); for (int k = 0 ; k < nums.size ();k++){ if (nums[k] >target && nums[k] >=0 )break ; if (k>0 && nums[k] == nums[k-1 ])continue ; for (int i = k+1 ; i<nums.size ();i++){ if (nums[k]+nums[i] > target && nums[k]+nums[i] >=0 )break ; if (i > k+1 && nums[i] == nums[i-1 ])continue ; int left = i+1 ; int right = nums.size ()-1 ; while (left<right){ if ((long )nums[k]+nums[i]+nums[left]+nums[right]>target)right--; else if ((long )nums[k]+nums[i]+nums[left]+nums[right]<target)left++; else { res.push_back (vector<int > {nums[k],nums[i],nums[left],nums[right]}); while (left<right && nums[left] == nums[left+1 ])left++; while (left<right && nums[right] == nums[right-1 ])right--; left++; right--; } } } } return res; } };
栈与队列
用栈实现队列
232. 用栈实现队列 - 力扣(LeetCode)
输入栈 输出栈 ,pop的时候要注意一下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class MyQueue {public : stack<int > stIn; stack<int > stOut; MyQueue () { } void push (int x) stIn.push (x); } int pop () if (stOut.empty ()) { while (!stIn.empty ()) { stOut.push (stIn.top ()); stIn.pop (); } } int result = stOut.top (); stOut.pop (); return result; } int peek () int res = this ->pop (); stOut.push (res); return res; } bool empty () return stIn.empty () && stOut.empty (); } };
用队列实现栈
225.用队列实现栈 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class MyStack {public : queue<int > que1; queue<int > que2; MyStack () { } void push (int x) que1. push (x); } int pop () int size = que1. size (); size--; while (size--) { que2. push (que1.f ront()); que1. pop (); } int result = que1.f ront(); que1. pop (); que1 = que2; while (!que2. empty ()) { que2. pop (); } return result; } int top () return que1. back (); } bool empty () return que1. empty (); } };
有效的括号
20. 有效的括号 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : bool isValid (string s) if (s.size () % 2 == 1 )return false ; stack<int > st; for (int i = 0 ;i<s.size ();i++){ if (s[i] == '(' )st.push (')' ); else if (s[i] == '[' )st.push (']' ); else if (s[i] == '{' )st.push ('}' ); else if (st.empty () || st.top () != s[i])return false ; else st.pop (); } return st.empty (); } };
删除字符串中的所有相邻重复项
1047. 删除字符串中的所有相邻重复项 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : string removeDuplicates (string s) { stack<char > st; for (int i = 0 ; i<s.size ();i++){ if (st.empty () || st.top () != s[i]) st.push (s[i]); else st.pop (); } string res = "" ; while (!st.empty ()){ res+=st.top (); st.pop (); } reverse (res.begin (),res.end ()); return res; } };
逆波兰表达式求值
150. 逆波兰表达式求值 - 力扣(LeetCode)
用两个数记录栈顶元素,再去做操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : int evalRPN (vector<string>& tokens) stack<long long > st; for (int i = 0 ; i< tokens.size ();i++){ if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/" ){ int num1 = st.top (); st.pop (); int num2 = st.top (); st.pop (); if (tokens[i] == "+" ) st.push (num2 + num1); if (tokens[i] == "-" ) st.push (num2 - num1); if (tokens[i] == "*" ) st.push (num2 * num1); if (tokens[i] == "/" ) st.push (num2 / num1); }else { st.push (stoll (tokens[i])); } } return st.top (); } };
滑动窗口最大值
239. 滑动窗口最大值 - 力扣(LeetCode)
题解参考
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : vector<int > maxSlidingWindow (vector<int >& nums, int k) { vector<int > ans; deque<int > q; for (int i = 0 ;i< nums.size ();i++){ while (!q.empty () && nums[q.back ()] <= nums[i]){ q.pop_back (); } q.push_back (i); if (i-q.front () >=k){ q.pop_front (); } if (i>=k-1 ){ ans.push_back (nums[q.front ()]); } } return ans; } };
前K个高频元素
347. 前 K 个高频元素 - 力扣(LeetCode)
要统计元素出现频率(map)
对频率排序(堆——优先队列)
找出前K个高频元素(小根堆)
如果采用大根堆,在每次移动更新大根堆的时候,每次弹出都把最大的元素弹出去,无法保留前K个高频元素
所以我们要用小根堆,因为要统计最大前k个元素,只有小根堆每次将最小的元素弹出,最后小根堆里积累的才是前k个最大元素
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public : vector<int > topKFrequent (vector<int >& nums, int k) { class mycomparison { public : bool operator () (const pair<int , int >& lhs, const pair<int , int >& rhs) return lhs.second > rhs.second; } }; unordered_map<int ,int > mp; for (int i= 0 ; i< nums.size ();i++){ mp[nums[i]]++; } priority_queue<pair<int ,int >,vector<pair<int ,int >>,mycomparison> pq; for (unordered_map<int ,int >::iterator it = mp.begin ();it != mp.end ();it++){ pq.push (*it); if (pq.size ()>k) pq.pop (); } vector<int > result; for (int i = k - 1 ; i >= 0 ; i--) { result[i] = pq.top ().first; pq.pop (); } return result; } };
二叉树
二叉树理论基础
二叉树种类
解题过程中常见的两种形式:满二叉树和完全二叉树
满二叉树
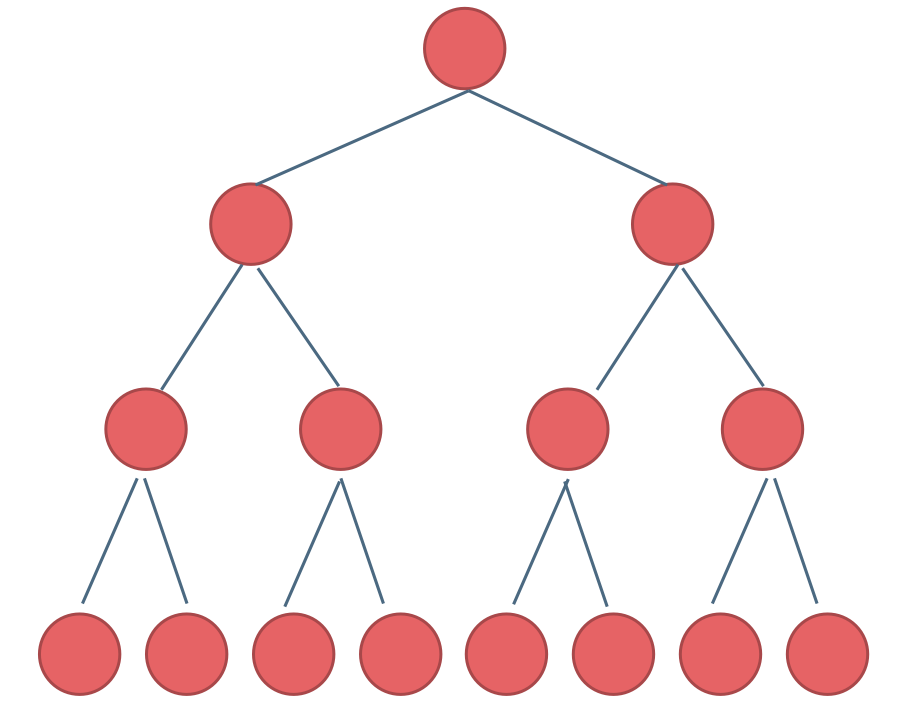
满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
完全二叉树
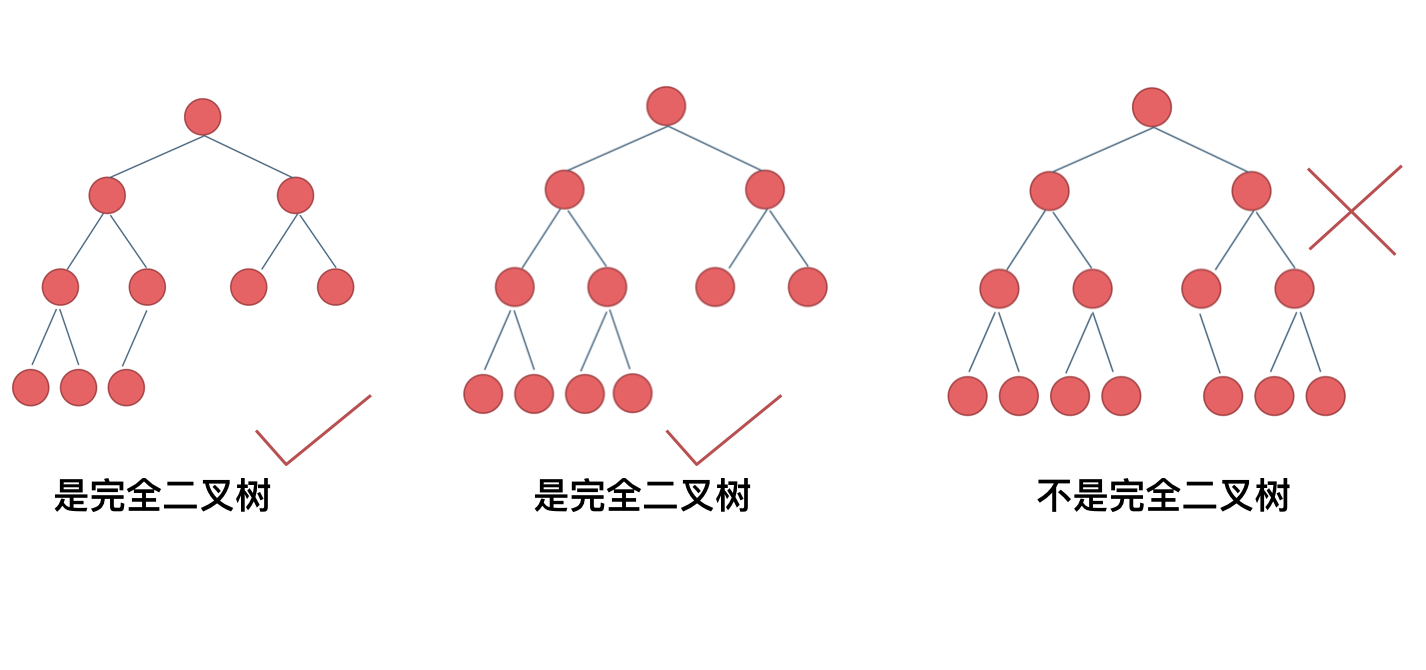
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
我来举一个典型的例子如题:
优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系
二叉搜索树
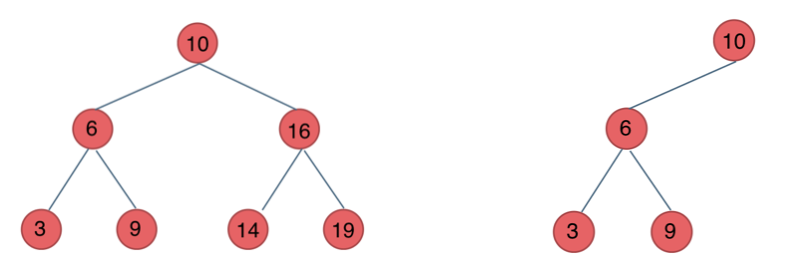
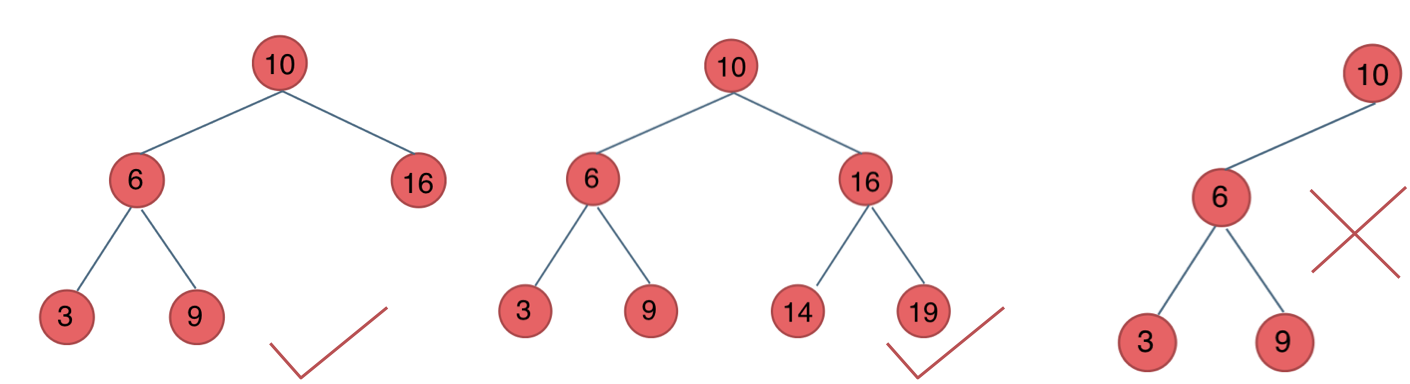
二叉搜索树是有数值的,二叉搜索树是一个有序树 。
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉排序树
下面这两棵树都是搜索树
平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
如图:
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树 ,所以map、set的增删操作时间时间复杂度是log(n),unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表。
二叉树的存储方式
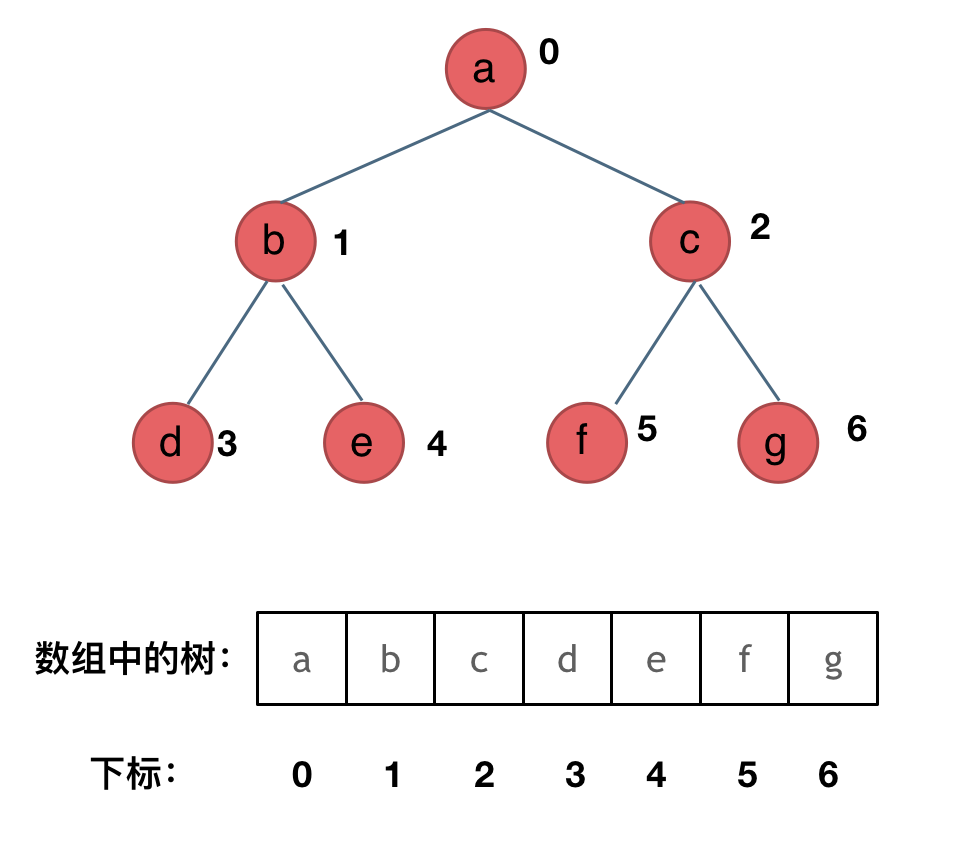
二叉树可以链式存储,也可以顺序存储。
那么链式存储方式就用指针, 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的,而链式存储则是通过指针把分布在各个地址的节点串联一起。
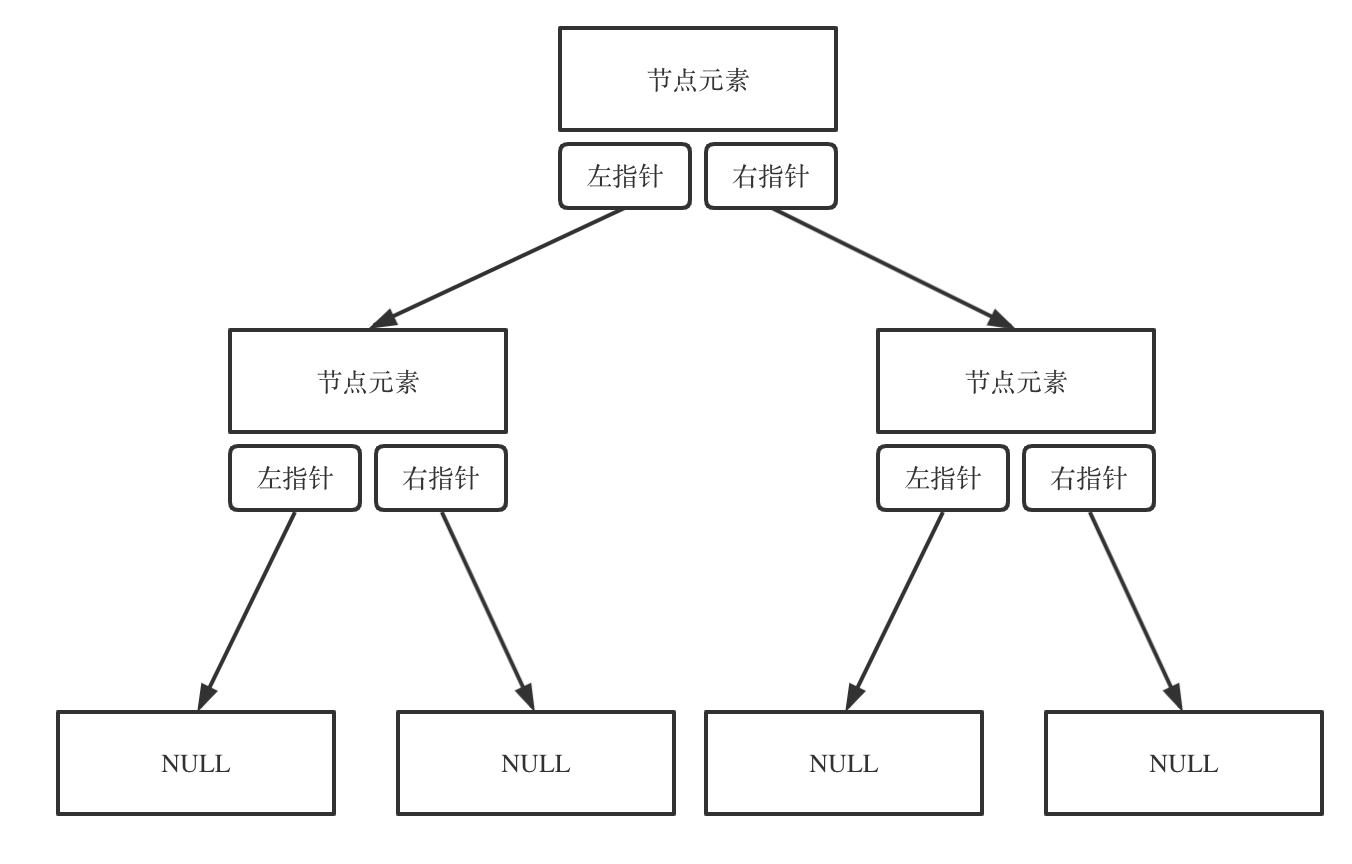
链式存储如图:
用数组来存储二叉树,顺序存储的方式如图:
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
二叉树的遍历方式
二叉树主要由两种遍历方式:
深度优先遍历:先往深走,遇到叶子节点再往回走。
广度优先遍历:一层一层的去遍历。
深度优先遍历
前序遍历(递归法,迭代法)中左右
中序遍历(递归法,迭代法)中左右
后序遍历(递归法,迭代法)中左右
广度优先遍历
这里前中后,其实指的就是中间节点的遍历顺序 ,只要大家记住 前中后序指的就是中间节点的位置就可以了。
二叉树定义
1 2 3 4 5 6 struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode (int x):val (x),left (NULL ),right (NULL ){} };
二叉树的递归遍历
递归三要素:
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
144. 二叉树的前序遍历 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : void func (TreeNode* cur,vector<int >& ans) if (cur == nullptr )return ; ans.push_back (cur->val); func (cur->left,ans); func (cur->right,ans); } vector<int > preorderTraversal (TreeNode* root) { vector<int >res; func (root,res); return res; } };
145. 二叉树的后序遍历 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : void func (TreeNode* cur,vector<int >& ans) if (cur == nullptr )return ; ans.push_back (cur->val); func (cur->left,ans); func (cur->right,ans); } vector<int > preorderTraversal (TreeNode* root) { vector<int >res; func (root,res); return res; } };
94. 二叉树的中序遍历 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : void func (TreeNode* cur,vector<int >& ans) if (cur == nullptr )return ; func (cur->left,ans); ans.push_back (cur->val); func (cur->right,ans); } vector<int > inorderTraversal (TreeNode* root) { vector<int > res; func (root,res); return res; } };
二叉树的迭代遍历
先将根节点放入栈中,然后将右孩子加入栈,再加入左孩子
这样出栈时的顺序为 中,左,右
144. 二叉树的前序遍历 - 力扣(LeetCode) s
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : vector<int > preorderTraversal (TreeNode* root) { stack<TreeNode*> st; vector<int > res; if (root == nullptr )return res; st.push (root); while (!st.empty ()){ TreeNode* tmp = st.top (); st.pop (); res.push_back (tmp->val); if (tmp->right)st.push (tmp->right); if (tmp->left)st.push (tmp->left); } return res; } };
94. 二叉树的中序遍历 - 力扣(LeetCode)
在这种情形下,处理顺序和访问顺序时不一致的,所以要改造一下
指针——访问节点,栈——处理节点
首先依次访问左边节点直至为NULL,取出栈顶指针,弹栈,加入答案,再访问右边节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : vector<int > inorderTraversal (TreeNode* root) { vector<int > res; stack<TreeNode*> st; TreeNode* cur = root; while ( !st.empty () || cur != nullptr ){ if (cur){ st.push (cur); cur = cur->left; }else { cur = st.top (); st.pop (); res.push_back (cur->val); cur = cur->right; } } return res; } };
145. 二叉树的后序遍历 - 力扣(LeetCode)
后序: 左,右,中,前序:中,左,右
在刚刚迭代方法实现前序遍历的基础上 先变一下顺序再翻转即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : vector<int > postorderTraversal (TreeNode* root) { stack<TreeNode*> st; vector<int > res; if (root == nullptr )return res; st.push (root); while (!st.empty ()){ TreeNode* cur = st.top (); st.pop (); res.push_back (cur->val); if (cur->left)st.push (cur->left); if (cur->right)st.push (cur->right); } reverse (res.begin (),res.end ()); return res; } };
589. N 叉树的前序遍历 - 力扣(LeetCode)
注意for循环里面的内容,倒序遍历才能保证出栈的时候是正确的顺序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : vector<int > preorder (Node* root) { stack<Node*> st; vector<int > res; if (root)st.push (root); while (!st.empty ()){ Node* cur = st.top (); st.pop (); res.push_back (cur->val); for (int i = cur->children.size ()-1 ; i>=0 ;i--){ if (cur->children[i])st.push (cur->children[i]); } } return res; } };
590. N 叉树的后序遍历 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : vector<int > postorder (Node* root) { stack<Node*> st; vector<int > res; if (root)st.push (root); while (!st.empty ()){ Node* cur = st.top (); st.pop (); res.push_back (cur->val); for (int i = 0 ; i< cur->children.size ();i++){ if (cur->children[i])st.push (cur->children[i]); } } reverse (res.begin (),res.end ()); return res; } };
二叉树的层序遍历
102. 二叉树的层序遍历 - 力扣(LeetCode)
队列先进先出,符合一层一层遍历的逻辑
而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : vector<vector<int >> levelOrder (TreeNode* root) { queue<TreeNode*> que; vector<vector<int >> res; if (root)que.push (root); while (!que.empty ()){ int size = que.size (); vector<int > ans; for (int i = 0 ; i < size;i++){ TreeNode* tmp = que.front (); que.pop (); ans.push_back (tmp->val); if (tmp->left)que.push (tmp->left); if (tmp->right)que.push (tmp->right); } res.push_back (ans); } return res; } };
107. 二叉树的层序遍历 II - 力扣(LeetCode)
reverse一下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : vector<vector<int >> levelOrderBottom (TreeNode* root) { queue<TreeNode*> que; vector<vector<int >> res; if (root)que.push (root); while (!que.empty ()){ int size = que.size (); vector<int > ans; for (int i = 0 ; i< size;i++){ TreeNode* tmp = que.front (); que.pop (); ans.push_back (tmp->val); if (tmp->left)que.push (tmp->left); if (tmp->right)que.push (tmp->right); } res.push_back (ans); } reverse (res.begin (),res.end ()); return res; } };
199. 二叉树的右视图 - 力扣(LeetCode)
层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : vector<int > rightSideView (TreeNode* root) { queue<TreeNode*> que; vector<int > res; if (root)que.push (root); while (! que.empty ()){ int size = que.size (); for (int i = 0 ; i< size;i++){ TreeNode* tmp = que.front (); que.pop (); if (i == size-1 )res.push_back (tmp->val); if (tmp->left)que.push (tmp->left); if (tmp->right)que.push (tmp->right); } } return res; } };
637. 二叉树的层平均值 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : vector<double > averageOfLevels (TreeNode* root) { queue<TreeNode*> que; vector<double > res; if (root)que.push (root); while (!que.empty ()){ int size = que.size (); double sum = 0 ; for (int i = 0 ; i< size;i++){ TreeNode* tmp = que.front (); que.pop (); sum += tmp->val; if (tmp->left)que.push (tmp->left); if (tmp->right)que.push (tmp->right); } res.push_back (sum/size); } return res; } };
429. N 叉树的层序遍历 - 力扣(LeetCode)
遍历孩子节点即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : vector<vector<int >> levelOrder (Node* root) { queue<Node*> que; vector<vector<int >> res; if (root)que.push (root); while (!que.empty ()){ int size = que.size (); vector<int > ans; for (int i = 0 ;i < size;i++){ Node* tmp = que.front (); que.pop (); ans.push_back (tmp->val); for (int i = 0 ; i< tmp->children.size ();i++){ if (tmp->children[i])que.push (tmp->children[i]); } } res.push_back (ans); } return res; } };
515. 在每个树行中找最大值 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : vector<int > largestValues (TreeNode* root) { queue<TreeNode*> que; vector<int > res; if (root)que.push (root); while (!que.empty ()){ int size = que.size (); int max = INT_MIN; for (int i =0 ; i<size;i++){ TreeNode* tmp = que.front (); que.pop (); max = tmp->val> max? tmp->val:max; if (tmp->left)que.push (tmp->left); if (tmp->right)que.push (tmp->right); } res.push_back (max); } return res; } };
116. 填充每个节点的下一个右侧节点指针 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution {public : Node* connect (Node* root) { queue<Node*> que; if (root)que.push (root); while (!que.empty ()){ int size = que.size (); Node* nodepre; Node* cur; for (int i = 0 ; i< size;i++){ if (i == 0 ){ nodepre = que.front (); que.pop (); cur = nodepre; }else { cur = que.front (); que.pop (); nodepre->next = cur; nodepre = nodepre->next; } if (cur->left)que.push (cur->left); if (cur->right)que.push (cur->right); } nodepre->next = NULL ; } return root; } };
117. 填充每个节点的下一个右侧节点指针 II - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution {public : Node* connect (Node* root) { queue<Node*> que; if (root)que.push (root); while (!que.empty ()){ Node* nodepre; Node* cur; int size = que.size (); for (int i =0 ; i< size;i++){ if (i == 0 ){ nodepre = que.front (); que.pop (); cur = nodepre; }else { cur = que.front (); que.pop (); nodepre->next = cur; nodepre = nodepre->next; } if (cur->left)que.push (cur->left); if (cur->right)que.push (cur->right); } nodepre->next = NULL ; } return root; } };
104. 二叉树的最大深度 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : int maxDepth (TreeNode* root) queue<TreeNode*> que; if (root)que.push (root); int cnt = 0 ; while (!que.empty ()){ int size = que.size (); cnt++; for (int i = 0 ; i< size;i++){ TreeNode* cur = que.front (); que.pop (); if (cur->left)que.push (cur->left); if (cur->right)que.push (cur->right); } } return cnt; } };
111. 二叉树的最小深度 - 力扣(LeetCode)
只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int minDepth (TreeNode* root) queue<TreeNode*> que; if (root)que.push (root); int cnt = 0 ; while (!que.empty ()){ int size = que.size (); cnt++; for (int i = 0 ; i< size;i++){ TreeNode* cur = que.front (); que.pop (); if (cur->left)que.push (cur->left); if (cur->right)que.push (cur->right); if (!cur->left && !cur->right)return cnt; } } return cnt; } };
翻转二叉树
226. 翻转二叉树 - 力扣(LeetCode)
把每个结点的左右孩子换个位置就行
1 2 3 4 5 6 7 8 9 10 class Solution {public : TreeNode* invertTree (TreeNode* root) { if (!root)return root; swap (root->left,root->right); invertTree (root->left); invertTree (root->right); return root; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : TreeNode* invertTree (TreeNode* root) { stack<TreeNode*> st; if (root)st.push (root); while (!st.empty ()){ TreeNode* tmp = st.top (); st.pop (); swap (tmp->left,tmp->right); if (tmp->left)st.push (tmp->left); if (tmp->right)st.push (tmp->right); } return root; } };
对称二叉树
101. 对称二叉树 - 力扣(LeetCode)
判断二叉树是否对称:比较的不是左右节点,而是左右子树
不但要遍历两棵树而且要比较内侧和外侧节点
确定终止条件:
节点为空的情况:(注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点 )
左节点为空,右节点不为空,不对称,return false
左不为空,右为空,不对称 return false
左右都为空,对称,返回true
左右节点不为空:
左右都不为空,比较节点数值,不相同就return false
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : bool func (TreeNode* left,TreeNode* right) if (!left && !right)return true ; else if (!left && right)return false ; else if (left && !right)return false ; else if (left->val != right->val)return false ; bool out = func (left->left,right->right); bool in = func (left->right,right->left); return out && in; } bool isSymmetric (TreeNode* root) bool ans = func (root->left,root->right); return ans; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public : bool isSymmetric (TreeNode* root) if (!root)return true ; queue<TreeNode*> que; que.push (root->left); que.push (root->right); while (!que.empty ()){ TreeNode* leftnode = que.front ();que.pop (); TreeNode* rightnode = que.front ();que.pop (); if (!leftnode && !rightnode)continue ; if (!leftnode ||! rightnode ||(leftnode->val != rightnode->val))return false ; que.push (leftnode->left); que.push (rightnode->right); que.push (leftnode->right); que.push (rightnode->left); } return true ; } };
二叉树的最大深度
104. 二叉树的最大深度 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : int maxDepth (TreeNode* root) queue<TreeNode*> que; if (root)que.push (root); int cnt = 0 ; while (!que.empty ()){ int size = que.size (); cnt++; for (int i = 0 ; i< size;i++){ TreeNode* cur = que.front (); que.pop (); if (cur->left)que.push (cur->left); if (cur->right)que.push (cur->right); } } return cnt; } };
559. N 叉树的最大深度 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : int maxDepth (Node* root) int sum = 0 ; queue<Node*> que; if (!root)return 0 ; que.push (root); while (!que.empty ()){ sum++; int size = que.size (); for (int i = 0 ; i < size;i++){ Node* tmp = que.front (); que.pop (); for (int i = 0 ; i < tmp->children.size ();i++){ if (tmp->children[i])que.push (tmp->children[i]); } } } return sum; } };
二叉树的最小深度
111. 二叉树的最小深度 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int minDepth (TreeNode* root) queue<TreeNode*> que; if (root)que.push (root); int cnt = 0 ; while (!que.empty ()){ int size = que.size (); cnt++; for (int i = 0 ; i< size;i++){ TreeNode* cur = que.front (); que.pop (); if (cur->left)que.push (cur->left); if (cur->right)que.push (cur->right); if (!cur->left && !cur->right)return cnt; } } return cnt; } };
完全二叉树的节点个数
222. 完全二叉树的节点个数 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : int func (TreeNode* cur) if (!cur)return 0 ; int lcnt = func (cur->left); int rcnt = func (cur->right); return lcnt+rcnt+1 ; } int countNodes (TreeNode* root) return func (root); } };
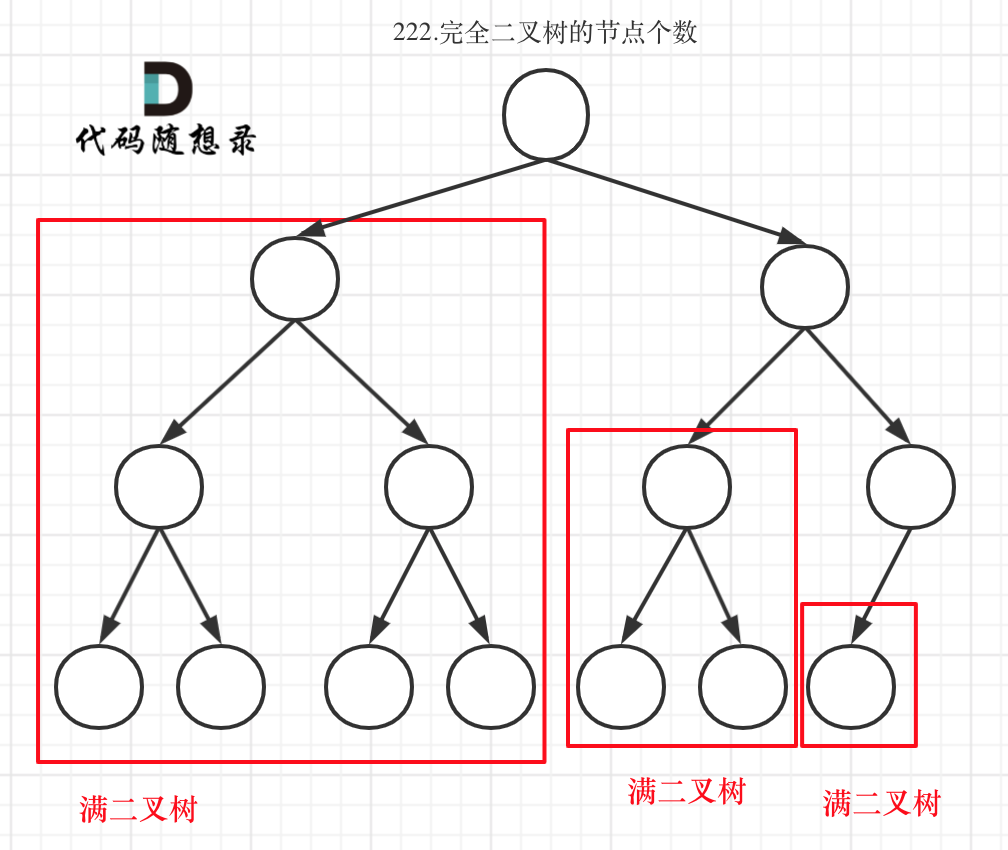
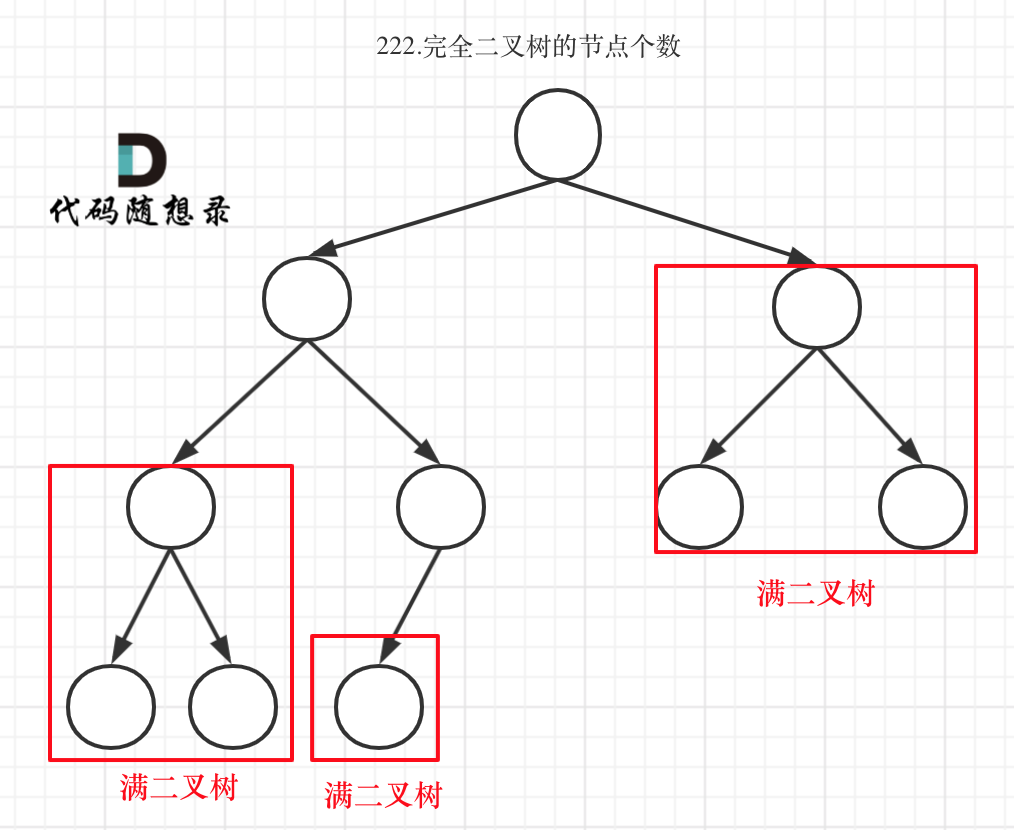
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树 ,然后依然可以按照情况一来计算
见下图:
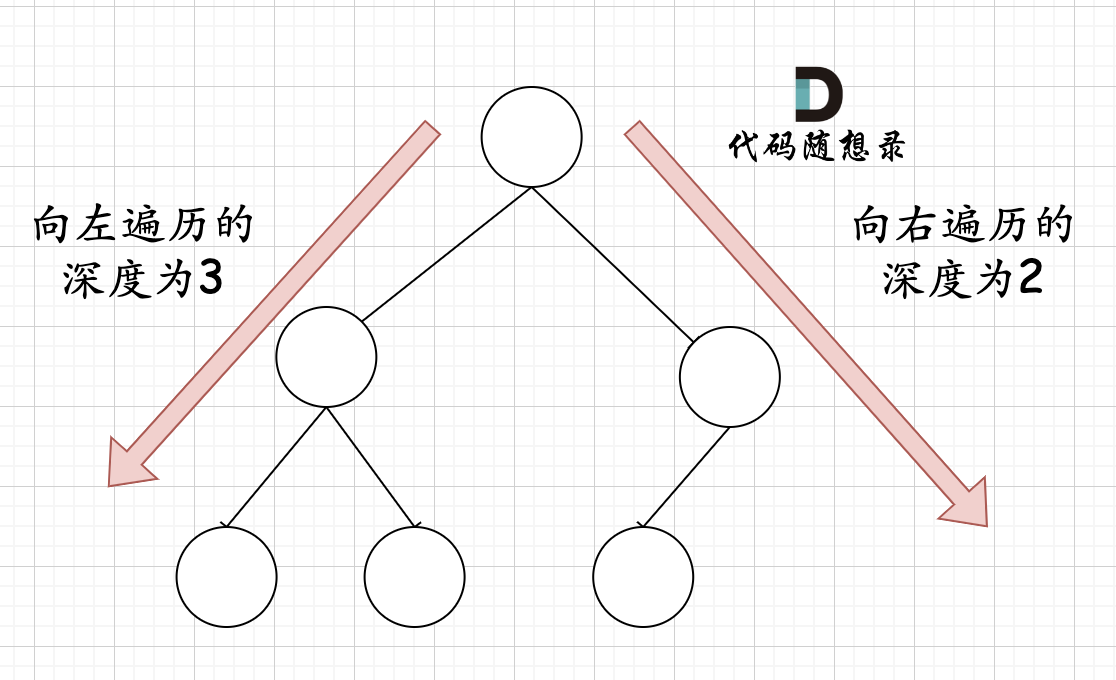
Q:关键在于如何去判断一个左子树或者右子树是不是满二叉树呢?
A:如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : int countNodes (TreeNode* root) if (root == nullptr ) return 0 ; TreeNode* left = root->left; TreeNode* right = root->right; int leftDepth = 0 , rightDepth = 0 ; while (left) { left = left->left; leftDepth++; } while (right) { right = right->right; rightDepth++; } if (leftDepth == rightDepth) { return (2 << leftDepth) - 1 ; } return countNodes (root->left) + countNodes (root->right) + 1 ; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int countNodes (TreeNode* root) int sum = 0 ; queue<TreeNode*> que; if (!root)return 0 ; que.push (root); while (!que.empty ()){ int size = que.size (); for (int i = 0 ; i < size;i++){ sum++; TreeNode* tmp= que.front (); que.pop (); if (tmp->left)que.push (tmp->left); if (tmp->right)que.push (tmp->right); } } return sum; } };
平衡二叉树
110. 平衡二叉树 - 力扣(LeetCode)
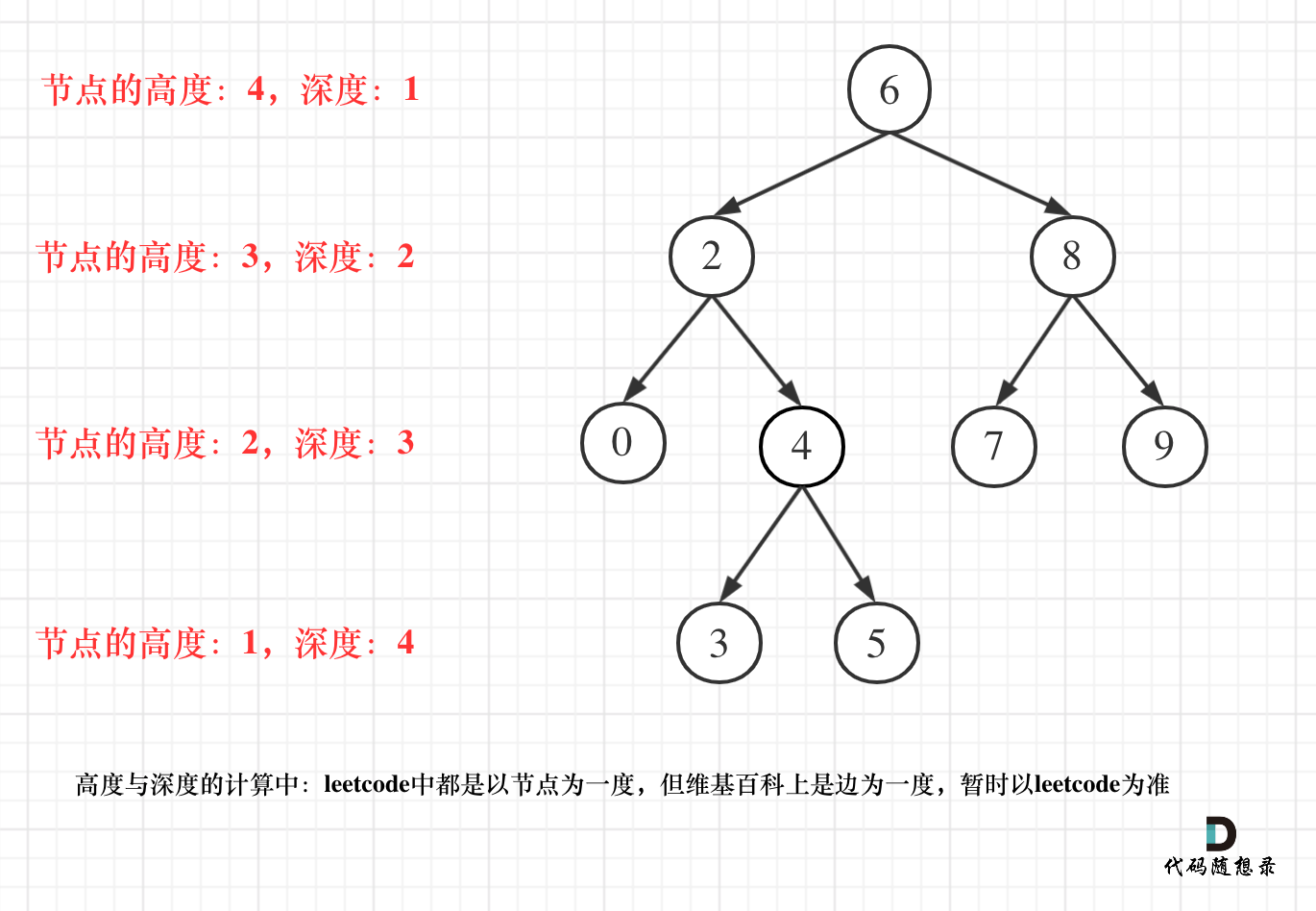
一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1
二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
【求深度——前序,求高度——后序】
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : int getHeight (TreeNode* node) if (node == NULL ) { return 0 ; } int leftHeight = getHeight (node->left); if (leftHeight == -1 ) return -1 ; int rightHeight = getHeight (node->right); if (rightHeight == -1 ) return -1 ; return abs (leftHeight - rightHeight) > 1 ? -1 : 1 + max (leftHeight, rightHeight); } bool isBalanced (TreeNode* root) return getHeight (root) == -1 ? false : true ; } };
二叉树的所有路径
257. 二叉树的所有路径 - 力扣(LeetCode)
递归+回溯 前序遍历(从根节点开始找)
三部曲:
确定参数:传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值
出口:(找叶子节点)——当cur不为空时,其左右孩子都为空的时候,就找到了叶子节点
单层递归逻辑:先处理中间节点,递归(在递归前判断cur是否为空),回溯(回溯要和递归永远在一起 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution {private : void traversal (TreeNode* cur, vector<int >& path, vector<string>& result) path.push_back (cur->val); if (cur->left == NULL && cur->right == NULL ) { string sPath; for (int i = 0 ; i < path.size () - 1 ; i++) { sPath += to_string (path[i]); sPath += "->" ; } sPath += to_string (path[path.size () - 1 ]); result.push_back (sPath); return ; } if (cur->left) { traversal (cur->left, path, result); path.pop_back (); } if (cur->right) { traversal (cur->right, path, result); path.pop_back (); } } public : vector<string> binaryTreePaths (TreeNode* root) { vector<string> result; vector<int > path; if (root == NULL ) return result; traversal (root, path, result); return result; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : void func (TreeNode* cur,string path, vector<string>& res) path += to_string (cur->val); if (!cur->left && !cur->right){ res.push_back (path); return ; } if (cur->left)func (cur->left,path+"->" ,res); if (cur->right)func (cur->right,path+"->" ,res); } vector<string> binaryTreePaths (TreeNode* root) { vector<string> res; string path; if (!root)return res; func (root,path,res); return res; } };
左叶子之和
404. 左叶子之和 - 力扣(LeetCode)
左叶子:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
因此判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子
确定参数返回值:根节点和int
递归出口:遍历到空节点时,左叶子值一定为0
单层逻辑:当遇到左叶子节点的时候,记录数值,然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : int sumOfLeftLeaves (TreeNode* root) if (!root)return 0 ; if (!root->left && !root->right)return 0 ; int sum = 0 ; int left_val = sumOfLeftLeaves (root->left); if (root->left && !root->left->left && !root->left->right){ left_val = root->left->val; } int right_val = sumOfLeftLeaves (root->right); return left_val+ right_val; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : int sumOfLeftLeaves (TreeNode* root) stack<TreeNode*> st; if (!root)return 0 ; st.push (root); int sum=0 ; while (!st.empty ()){ TreeNode* cur = st.top (); st.pop (); if (cur->left && !cur->left->left && !cur->left->right) sum+=cur->left->val; if (cur->left)st.push (cur->left); if (cur->right)st.push (cur->right); } return sum; } };
找树左下角的值
513. 找树左下角的值 - 力扣(LeetCode)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int findBottomLeftValue (TreeNode* root) queue<TreeNode*> que; int res; if (!root)return 0 ; que.push (root); while (!que.empty ()){ int size = que.size (); for (int i = 0 ; i< size;i++){ TreeNode* tmp = que.front (); que.pop (); if (i == 0 )res = tmp->val; if (tmp->left)que.push (tmp->left); if (tmp->right)que.push (tmp->right); } } return res; } };
路径总和
112. 路径总和 - 力扣(LeetCode)
递归三部曲:
根节点root,计数器count,返回值为bool
让计数器count初始为目标和,然后每次减去遍历路径节点上的数值。
当遇到叶子节点且count==0时,返回true,反之false
回溯!!
递归函数什么时候需要返回值?什么时候不需要返回值?这里总结如下三点:
如果需要搜索整棵二叉树且不用 处理递归返回值,递归函数就不要返回值
如果需要搜索整棵二叉树且需要 处理递归返回值,递归函数就需要返回值。
如果要搜索其中一条符合条件的路径 ,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(本题的情况)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution {public : bool func (TreeNode* cur,int sum) if (!cur->left && !cur->right && sum == 0 )return true ; if (!cur->left && cur->right)return false ; if (cur->left){ sum -= cur->left->val; if (func (cur->left,sum))return true ; sum+=cur->left->val; } if (cur->right){ sum -= cur->right->val; if (func (cur->right,sum))return true ; sum+=cur->right->val; } return false ; } bool hasPathSum (TreeNode* root, int targetSum) if (!root)return false ; return func (root,targetSum); } };
113. 路径总和 II - 力扣(LeetCode)